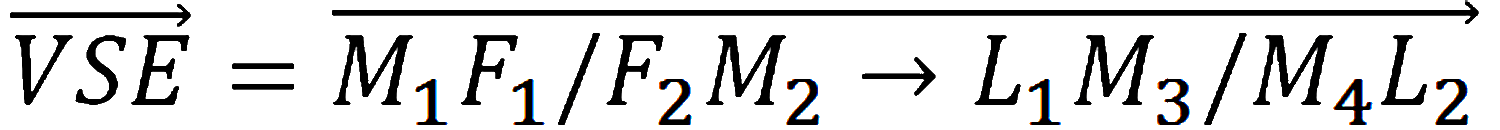
A uno sguardo storico sufficientemente limpido si mostra con distinzione che una sola e identica impulsione di pensiero – qui, il vettore storico-epistemologico "VSE" – è quella che dal seno della scienza antica genera dapprima la scienza moderna grazie all’opera di matematizzazione della Fisica/fisicizzazione della Matematica compiuta dai pensatori di fine XVI/XVII secolo, per poi propellere, due secoli dopo, la scienza contemporanea, grazie al lavoro di logicizzazione della Matematica/ matematizzazione della Logica, compiuta dai pensatori del XIX/inizio XX secolo. Con una formula di sintesi scrivo: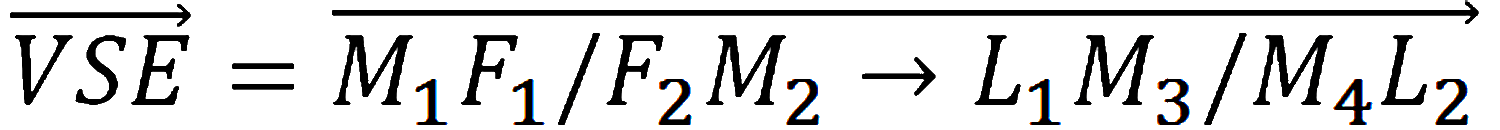
<1> GALILEO - "[A] Salviati Adunque se voi stabilirete alcun punto per capo e termine delle misure, e da esso farete partire una retta linea come determinatrice della prima misura, cioè della lunghezza, bisognerà per necessità che quella che dee definir la larghezza si parta ad angolo retto sopra la prima, e che quella che ha da notar l'altezza, che è la terza dimensione, partendo dal medesimo punto formi, pur con le altre due, angoli non obliqui, ma retti: e cosí dalle tre perpendicolari avrete, come da tre linee une e certe e brevissime, determinate le tre dimensioni, A B lunghezza, A C larghezza, A D altezza.
E perché chiara cosa è, che al medesimo punto non può concorrere altra linea che con quelle faccia angoli retti, e le dimensioni dalle sole linee rette che tra di loro fanno angoli retti deono esser determinate, adunque le dimensioni non sono piú che 3; e chi ha le 3 le ha tutte, e chi le ha tutte è divisibile per tutti i versi, e chi è tale è perfetto, etc. SIMP. E chi lo dice che non si possan tirare altre linee? e perché non poss'io far venir di sotto un'altra linea sino al punto A, che sia a squadra con l'altre? SALV. Voi non potete sicuramente ad un istesso punto far concorrere altro che tre linee rette sole, che fra di loro costituiscano angoli retti. SAGR. Sí, perché quella che vuol dire il signor Simplicio par a me che sarebbe l'istessa D A prolungata in giú: ed in questo modo si potrebbe tirarne altre due, ma sarebbero le medesime prime tre, non differenti in altro, che dove ora si toccano solamente, all'ora si segherebbero, ma non apporterebbero nuove dimensioni.
[B] Simplicio - Io non dirò che questa vostra ragione non possa esser concludente, ma dirò bene con Aristotile che nelle cose naturali non si deve sempre ricercare una necessità di dimostrazion matematica. SAGREDO Sí, forse, dove la non si può avere; ma se qui ella ci è, perché non la volete voi usare? Ma sarà bene non ispender piú parole in questo particolare, perché io credo che il signor Salviati ad Aristotile ed a voi senza altre dimostrazioni avrebbe conceduto, il mondo esser corpo, ed esser perfetto e perfettissimo, come opera massima di Dio." [Galileo 1632:14]
Fissiamo innanzitutto la più-che-logico/matematicamente rigorosa identità/continuità d'impulsione razionale di cui è qui questione, nel vettore matematizzazione1 --> matematizzazione2 che conduce dallo scambio Salviati-Simplicio in <1>, allo scambio Dedekind-Lipschitz in <2>:
<2> [A] DEDEKIND« Euclide passe totalement sous silence ce point important pour l’Arithmétique, et c’est pourquoi je ne peux pas vous suivre. […] Qu’en est-il d’Euclide à ce sujet ? Que l’on analyse toutes les hypothèses, tant les explicites que les implicites sur lesquelles repose l’ensemble de l’édifice de la géométrie d’Euclide, que l’on accorde la vérité de tous ses théorèmes […] : jamais on ne parvient de cette façon à la continuité de l’espace en tant que condition indissolublement liée à la géométrie d’Euclide» [Dedekind 1876b : 56]
[B] LIPSCHITZ « Je sais fort bien que vous objecterez qu’il ne vous suffit pas de déduire l’existence d’un rapport à partir d’une construction géométrique. À quoi je réponds ceci. L’esprit humain a tiré les forces qu’il possède actuellement pour une grande part de l’exercice de la géométrie. Le rigor geometricus a passé durant des millénaires pour l’exigence la plus haute. Si aujourd’hui nous formulons d’autres exigences, nous en sommes redevables pour l’essentiel à l’exercice de la géométrie, et ces exigences ne sont pas non plus intrinsèquement différentes aujourd’hui. Celui qui ne veut pas dire que la diagonale de ce carré est v2, ne saurait cependant nier qu’il est impossible que (m/n)2=2 pour des entiers m et n, et il doit admettre qu’on peut satisfaire les inégalités (m/n)2-2 > 0 et (m/n)2-2 < 0 avec toute la précision voulue. Cela aussi les anciens nous l’ont enseigné, et la définition de votre coupure a-t-elle une teneur différente ? Je pense que non. » [R. Lipschitz à R. Dedekind, le 6/7/1876 - Dedekind 1876 : 48]
In questo scambio, Dedekind presentifica la stessa "esigenza di matematica" che Salviati incarna e Sagredo difende nel passo precedente, mentre dal canto suo Lipschitz risponde con la stessa perplessa indifferenza e dogmatica venerazione degli "antichi" che in quel caso aveva animato la risposta di Simplicio.
Ora, si deve mettere tra virgolette l'espressione "esigenza di matematica" o di "matematizzazione", perché la continuità/identità interna di questa spinta propulsiva che attraversa i secoli non può esser colta se non come un'ininterrotta dinamica di re-significazione del concetto stesso di "matematica".
Nel passo galileiano, infatti, noi riconosciamo immediatamente l'evento di un'effettiva matematizzazione, che si produce sotto gli occhi di qualcuno che non ne comprende né la necessità contingente né il senso profondo. La stuazione gode in questo caso della massima distinzione - anche per contrasto - perché si tratta in effetti di applicare la Matematica come scienza à se stante a una Fisica ancora non "matematizzata" (per Simplicio è immediatamente ovvio che la Matematica non è la Fisica, così come il Moto non è la Quiete).
Nello scambio Dedekind/Lipschitz al contrario, ci muoviamo interamente all'interno della Matematica stessa, in un modo scientifico già integralmente "matematizzato": il dialogo avviene in questo caso tra due eminenti e riconosciuti matematici, e la spinta dedekindiana a una "vera" dimostrazione, che possa cioè dirsi logicamente corretta e dunque autenticamente "matematica", di ciò che per contro appare al collega come già largamente dimostrato da millenni, viene per questo classificata a seconda dei contesti come una speciazione interna al genus "Matematica": "aritmetizzazione", "logicizzazione" "rigorizzazione"... [1]
«Le souvenir du changement opéré par le premier pas fait dans cette route nouvellement découverte, a dû paraître extrêmement important aux mathématiciens, et a été sauvé par cela de l'oubli. Le premier qui démontra le triangle isocèle (qu'il s'appelât Thalès ou de tout autre nom) fut frappé d'une grande lumière ; car il trouva qu'il ne devait pas s'attacher à ce qu'il voyait dans la figure, ou même au simple concept qu'il en avait, mais qu'il n'avait qu'à dégager ce que lui-même y faisait entrer au moyen de ce qu'il pensait à ce sujet et se représentait a priori par concepts, et que, pour connaître avec certitude une chose a priori, il ne devait attribuer à cette chose que ce qui dérivait nécessairement de ce qu'il y avait mis lui-même, en conséquence de son concept. » [Kant 1787 : 43, BXIII.]
<3> GALILEO - SIMPLICIO - O io non sono un di quegli uomini che intendano, o 'n questo vostro discorso è una manifesta contradizione. Voi tra i maggiori encomii, anzi pur per il massimo di tutti, attribuite all'uomo, fatto dalla natura, questo dell'intendere; e poco fa dicevi con Socrate che 'l suo intendere non era nulla; adunque bisognerà dire che né anco la natura abbia inteso il modo di fare un intelletto che intenda. - SALVIATI Molto acutamente opponete; e per rispondere all'obbiezione, convien ricorrere a una distinzione filosofica, dicendo che l'intendere si può pigliare in due modi, cioè intensive, o vero extensive: e che extensive, cioè quanto alla moltitudine degli intelligibili, che sono infiniti, l'intender umano è come nullo, quando bene egli intendesse mille proposizioni, perché mille rispetto all'infinità è come un zero; ma pigliando l'intendere intensive, in quanto cotal termine importa intensivamente, cioè perfettamente, alcuna proposizione, dico che l'intelletto umano ne intende alcune cosí perfettamente, e ne ha cosí assoluta certezza, quanto se n'abbia l'istessa natura; e tali sono le scienze matematiche pure, cioè la geometria e l'aritmetica, delle quali l'intelletto divino ne sa bene infinite proposizioni di piú, perché le sa tutte, ma di quelle poche intese dall'intelletto umano credo che la cognizione agguagli la divina nella certezza obiettiva, poiché arriva a comprenderne la necessità, sopra la quale non par che possa esser sicurezza maggiore - SIMPLICIO. Questo mi pare un parlar molto resoluto ed ardito - SALVIATI Queste son proposizioni comuni e lontane da ogni ombra di temerità o d'ardire e che punto non detraggono di maestà alla divina sapienza, sí come niente diminuisce la Sua onnipotenza il dire che Iddio non può fare che il fatto non sia fatto. Ma dubito, signor Simplicio, che voi pigliate ombra per esser state ricevute da voi le mie parole con qualche equivocazione. Però, per meglio dichiararmi, dico che quanto alla verità di che ci danno cognizione le dimostrazioni matematiche, ella è l'istessa che conosce la sapienza divina; ma vi concederò bene che il modo col quale Iddio conosce le infinite proposizioni, delle quali noi conosciamo alcune poche, è sommamente piú eccellente del nostro, il quale procede con discorsi e con passaggi di conclusione in conclusione, dove il Suo è di un semplice intuito: e dove noi, per esempio, per guadagnar la scienza d'alcune passioni del cerchio, che ne ha infinite, cominciando da una delle piú semplici e quella pigliando per sua definizione, passiamo con discorso ad un'altra, e da questa alla terza, e poi alla quarta, etc., l'intelletto divino con la semplice apprensione della sua essenza comprende, senza temporaneo discorso, tutta la infinità di quelle passioni; le quali anco poi in effetto virtualmente si comprendono nelle definizioni di tutte le cose, e che poi finalmente, per esser infinite, forse sono una sola nell'essenza loro e nella mente divina. Il che né anco all'intelletto umano è del tutto incognito, ma ben da profonda e densa caligine adombrato, la qual viene in parte assottigliata e chiarificata quando ci siamo fatti padroni di alcune conclusioni fermamente dimostrate e tanto speditamente possedute da noi, che tra esse possiamo velocemente trascorrere: perché in somma, che altro è l'esser nel triangolo il quadrato opposto all'angolo retto eguale a gli altri due che gli sono intorno, se non l'esser i parallelogrammi sopra base comune e tra le parallele, tra loro eguali? e questo non è egli finalmente il medesimo che essere eguali quelle due superficie che adattate insieme non si avanzano, ma si racchiuggono dentro al medesimo termine? Or questi passaggi, che l'intelletto nostro fa con tempo e con moto di passo in passo, l'intelletto divino, a guisa di luce, trascorre in un instante, che è l'istesso che dire, gli ha sempre tutti presenti. Concludo per tanto, l'intender nostro, e quanto al modo e quanto alla moltitudine delle cose intese, esser d'infinito intervallo superato dal divino; ma non però l'avvilisco tanto, ch'io lo reputi assolutamente nullo; anzi, quando io vo considerando quante e quanto maravigliose cose hanno intese investigate ed operate gli uomini, pur troppo chiaramente conosco io ed intendo, esser la mente umana opera di Dio, e delle piú eccellenti.
<4> [A] RIEMANN «On sait que la Géométrie admet comme données préalables non seulement le concept de l’espace, mais encore les premières idées fondamentales des constructions dans l’espace. Elle ne donne de ces concepts que des définitions nominales, les déterminations essentielles s’introduisant sous forme d’axiomes. Les rapports mutuels de ces données primitives restent enveloppés de mystère ; on n’aperçoit pas bien si elles sont nécessairement liées entre elles, ni jusqu’à quel point elles le sont, ni même a priori si elles peuvent l’être. Depuis Euclide jusqu’à Legendre, pour ne citer que le plus illustre des réformateurs modernes de la Géométrie, personne, parmi les mathématiciens ni parmi les philosophes, n’est parvenu à éclaircir ce mystère. La raison en est que le concept général des grandeurs de dimensions multiples, comprenant comme cas parti d'une grandeur de dimensions multiples. Il ressortira de là qu'une grandeur de dimensions multiples est susceptible de différents rapports métriques, et que l'espace n'est par suite qu'un cas par¬ticulier d'une grandeur de trois dimensions » [Riemann 1854 : 280]
[B] EINSTEIN - «Sans doute avez-vous, cher lecteur, quand vous étiez jeune garçon, fait la connaissance du superbe édifice de la Géométrie d'Euclide, et vous vous rappelez peut-être, avec plus de respect que de plaisir, cette imposante construction sur le haut escalier de laquelle des maîtres consciencieux vous forçaient de monter pendant des heures innombrables. En vertu de ce passé vous traiteriez avec dédain toute personne qui regarderait même la moindre proposition de cette science comme inexacte. Mais ce sentiment de fière certitude vous abandonnerait peut-être, si l'on vous posait cette question : "Qu'entendez-vous par l'affirmation que ces propositions sont vraies ?" »[Einstein 1917 : 2]
[C] POINCARE - «Pour un observateur superficiel, la vérité scientifique est hors des atteintes du doute; la logique de la science est infaillible et, si les savants se trompent quelquefois, c'est pour en avoir méconnu les règles. Les vérités mathématiques dérivent d'un petit nombre de propositions évidentes par une chaîne de raisonnements impeccables; elles s'imposent non seulement à nous, mais à la nature elle-même. Elles enchaînent pour ainsi dire le Créateur et lui permettent seulement de choisir entre quelques solutions relativement peu nombreuses. Il suffira alors de quelques expériences pour nous faire savoir quel choix il a fait. De chaque expérience, une foule de conséquences pourront sortir par une série de déductions mathématiques, et c'est ainsi que chacune d'elles nous fera connaître un coin de l'Univers. Voilà quelle est pour bien des gens du monde, pour les lycéens qui reçoivent les premières notions de physique, l'origine de la certitude scientifique »[Poincaré 1902 : ...]
[D] EINSTEIN - «La géométrie part de certaines notions fondamentales telles que le point, la droite, le plan, auxquelles nous sommes capables d’associer des représentations plus ou moins claires, et de certaines propositions simples (axiomes), que nous sommes disposés à regarder, en vertu de ces représentations, comme «vraies ». Toutes les autres propositions sont ensuite ramenées, au moyen d’une méthode logique dont nous nous sentons forcés de reconnaître la légitimité, aux axiomes, c’est-à-dire démontrées. Une proposition est, par consé¬quent, exacte ou «vraie», si elle est déduite des axiomes de la manière généralement admise. La question de savoir si telle ou telle proposition géométrique est « vraie » se ramène, par conséquent, à la question de savoir si les axiomes sont « vrais ». Mais on sait depuis longtemps que non seulement on ne peut répondre à cette dernière question au moyen des méthodes de la géométrie, mais qu’elle n’a en elle-même aucun sens. On ne peut pas demander s’il est vrai que par deux points il ne passe qu’une seule droite. On peut seulement dire que la Géométrie euclidienne traite de figures qu’elle appelle « droites » et auxquelles elle attribue la propriété d’être déterminées d’une manière univoque par deux de ses points. La notion de « vrai » ne s’applique pas aux énoncés de la géométrie pure, car par le terme « vrai » nous désignons, en dernier ressort, toujours la concordance avec un objet « réel ». Or, la Géométrie ne s’occupe pas du rapport entre ses notions et les objets de l’expérience, mais seulement du rapport logique de ces notions entre elles. [Einstein 1917 ]
[E] POINCARE «La vérité nous effraie. Et en effet, nous savons qu’elle est quelquefois décevante, que c’est un fantôme qui ne se montre à nous un instant que pour fuir sans cesse, qu’il faut la poursuivre plus loin et toujours plus loin, sans jamais pouvoir l’atteindre. Et cependant pour agir il faut s’arrêter, ananké sténaï comme a dit je ne sais plus quel grec, Aristote ou un autre »[Poincaré 1905 : 18]
[F] RIEMANN « Le concept général des grandeurs de dimensions multiples, comprenant comme cas particulier les grandeurs étendues, n’a jamais été l’objet d’aucune étude. En conséquence, je me suis posé d’abord le problème de construire, en partant du concept général de grandeur, le concept d’une grandeur de dimensions multiples. Il ressortira de là qu’une grandeur de dimensions multiples est susceptible de différents rapports métriques, et que l’espace n’est par suite qu’un cas particulier d’une grandeur de trois dimensions. Or, il s’ensuit de là nécessairement que les propositions de la Géométrie ne peuvent se déduire des concepts généraux de grandeur, mais que les propriétés par lesquelles l’espace se distingue de toute autre grandeur imaginable de trois dimensions, ne peuvent être empruntées qu’à l’expérience. De là surgit le problème de rechercher les faits les plus simples au moyen desquels puissent s’établir les rapports métriques de l’espace, problème qui, par la nature même de l’objet, n’est pas complètement déterminé; car on peut indiquer plusieurs systèmes de faits simples, suffisants pour la détermination des rapports métriques de l’espace. Le plus important, pour notre but actuel, est celui qu’Euclide a pris pour base. [281] - ?2? Ces faits, comme tous les faits possibles, ne sont pas nécessaires; ils n’ont qu’une certitude empirique, ce sont des hypothèses. On peut donc étu¬dier leur probabilité, qui est certainement très considérable dans les limites de l'observation.» [Riemann 1854 : 280-1]
[G] La concezione antica della geometria, intesa come ricerca del “vero”, attraverso la razionalizzazione dell’esperienza sensibile dello spazio esterno, corrisponde all’ideale greco di una verità eterna e immortale. Noi abbiamo invece ora, come vedremo nei prossimi paragrafi, una concezione molto più ricca della geometria, in un certo senso più vicina al bisogno reale dell’uomo di oggi. […] La concezione odierna della geometria è molto più prudente, ma conduce molto più lontano. Dice all’incirca così: i punti e le rette sono schemi mentali che traducono in qualche modo le nostre esperienze visive e tattili. Conveniamo tra noi di ammettere, come un buon enunciato, chiaro e breve, che “per due punti passa una e una sola retta”. […] In tal modo la “verità” del nostro assioma è semplicemente il fatto che esso traduce bene le nostre esperienze spaziali. La “verità” delle nostre conseguenze logiche è invece il fatto che tutti i passaggi logici intermedi che dobbiamo compiere per ottenerle, sono gli stessi per tutte le menti (sane). Questo modo di pensare viene premiato dalla natura con un miracolo che si ripete ogni giorno milioni di volte, ovunque vi sia un essere umano che pensa e parla». [Melzi 1986: 10-13. Corsivi miei]
[H] «Cantor donne une définition du concept de ensemble que l’on peut appeler euclidienne, à savoir une définition qui devrait se trouver soit dans un dictionnaire linguistique soit dans un livre de philosophie, plutôt que dans un livre de mathématique. […] Les essais de présenter l’idée d’ensemble et d’élément d’un ensemble ne se sont encore pas conclus, ou de moins ils ne se sont pas achevés avec un accord de majorité partagé par les plus éminents spécialistes. Pour cette raison nous nous prendrons la liberté d’élargir l’idée d’ensemble»
DESCARTES«Toutes les questions que vous faites des bêtes sont hors de propos, et ce n'est pas ici le lieu de les examiner ; d'autant que l'esprit, méditant en soi- même et faisant réflexion sur ce qu'il est, peut bien expérimenter qu'il pense, mais non pas si les bêtes ont des pensées ou si elles n'en ont pas ; et il n'en peut rien découvrir que lorsque, examinant leurs opérations, il remonte des effets vers leurs causes [...] J'ai souvent apporté la véritable marque par laquelle nous pouvons connaitre que l'esprit est différent du corps, qui est que toute l'essence ou toute la nature de l'esprit consiste seulement à penser, là où toute la nature du corps consiste seulement en ce point, que le corps est une chose étendue, et aussi qu'il n'y a rien du tout de commun entre la pensée et l'extension. J'ai souvent aussi fait voir fort clairement que l'esprit peut agir indépendamment du cerveau ; car il est certain qu'il est de nul usage lorsqu'il s'agit de former des actes d'une pure intellection, mais seulement quand il est question de sentir ou d'imaginer quelque chose ; et bien que, lorsque le sentiment ou l'imagination est fortement agitée, comme il arrive quand le cerveau est troublé, l'esprit ne puisse pas facilement s'appliquer à concevoir d'autres choses, nous expérimentons néanmoins que, lorsque notre imagination n'est pas si forte, nous ne laissons pas souvent de concevoir quelque chose d'entièrement différent de ce que nous imaginons, comme lorsqu'au milieu de nos songes nous apercevons que nous rêvons ; car alors c'est bien un effet de notre imagination que nous rêvons, mais c'est un ouvrage qui n'appartient qu'à l'entendement seul de nous faire apercevoir de nos rêveries. [Descartes AT7:512]»
CAUCHY«Naissance d’une communaute scientifique. Facteurs d’unité. Si une culture encyclopédique restait la règle chez les savants, c'est qu'elle répondait a une curiosité. Elle ne signifiait pas qu'une structure unitaire gouvernait tout le savoir : comme nous le verrons plus loin, cette unité était abandonnée au sein de la philosophie naturelle. Il y avait spécialisation. Restait prégnante cependant l'idée d'un continuum intellectuel qui allait des mathématiques aux beaux-arts. Plus prosaïquement, on pourrait aussi avancer qu'une large culture des savants répondait au souci de ne pas paraitre inferieurs aux hommes de lettres. Si l'image des sciences était positive vers 1800, le modèle intellectuel restait l'écrivain : Voltaire ou Montesquieu. Rappelons la séance de l'Institut de 1798 où Laplace se permit d'intervenir dans des discussions sur le calorique et l'électricité chez les animaux, ou celle durant laquelle Laplace et Lamarck s'empoignèrent au sujet de la météorologie. Sous la Restauration, alors que l'on exposait la théorie des protubérances cérébrales de Gall, le ton avait déjà changé. Cauchy jugeait utile de prévenir : "Je n'ai pas la prétention de m'y connaitre en anatomie”, et il avançait une argumentation d'ordre philosophique : "Ce que le docteur Gall n'a jamais prouve et ne prouvera jamais, c’est que la diversité des pièces du cerveau matériel anéantisse l'unité du moi, c'est qu'on puisse disséquer la pensée, et lui assigner des formes géométriques"*[123. Académie des sciences, 19 juillet 1824, cite par B. Belhoste, Cauchy, un mathématicien légitimiste au xix` siècle, Paris, Belin, 1985, pp. 114-115] » [Dhombres 1989 : 208]
L'idea che si possa accedere all'evento individuale di una singola operazione matematica è una pura intenzione programmatica, attualmente non realizzata, e in linea di principio irrealizzabile. La "brain imagery" sta all' "atomo operatorio" che essa cerca di cogliere, come il "microscopio ideale" di Feynmann sta alle palline in computer-graphic che infestano i testi di Fisica e di chimica.
Chapitre 4 - Une approche neuroscientifique de l’apprentissage Les découvertes stimulantes de la neuroscience cognitive et les développements continus de la psychologie cognitive commencent à fournir des réflexions intéressantes sur les mécanismes d’apprentissage du cerveau. L’histoire nous enseigne que la théorie et la méthode ont séparé ces deux disciplines. Cependant, le développement de nouvelles technologies d’imagerie du cerveau a permis l’émergence d’une nouvelle science les combinant : la neuroscience cognitive. Les neuroscientifiques cognitifs accordent de plus en plus d’attention à l’éducation considérée en tant que champ d’application des connaissances neuroscientifiques et en tant que source de questions importantes pour la recherche. Dans ce chapitre sont résumées les recherches neuroscientifiques initialement présentées durant les trois forums internationaux dont il a été question plus haut. Bien que nombre de sujets différents y aient été discutés, on rapportera ici ceux dont les applications potentielles ont été jugées d’un grand intérêt et qui ont apporté des informations significatives en matière de définition de programmes, de pratiques de l’enseignement et de styles d’apprentissage. Parmi eux figurent : la littératie et la numératie, le rôle de l’émotionnel dans l’apprentissage et l’apprentissage tout au long de la vie. Mais avant de nous intéresser à la substance proprement dite, il semble nécessaire de présenter brièvement quelques principes de base sur l’architecture du cerveau, ainsi que les instruments de recherche (la technologie) et la méthodologie utilisés aujourd’hui par la neuroscience cognitive. A la fin de ce chapitre, on étudiera les « neuromythologies » fondées sur les erreurs de conception et/ou l’incompréhension populaires vis-à-vis de la science.
4.1. Principes de l’organisation du cerveau et du traitement neural de l’information - 4.1.1. Neurones, états mentaux, connaissance et apprentissage
Le composant fondamental du traitement de l’information dans le cerveau est le neurone, une cellule capable d’accumuler et de transmettre l’activité électrique. Un cerveau humain contient environ 100 milliards de neurones, dont chacun peut être connecté avec des milliers de ses semblables, ce qui permet aux signaux d’information de circuler massivement et dans plusieurs directions à la fois. A tout instant, un très grand nombre de neurones sont simultanément actifs, et chacune de ces « structures d’activité » correspond à un état mental déterminé. A mesure que l’électricité circule à travers les connexions entre neurones (ces connexions sont appelées synapses), un autre ensemble de neurones est activé et le cerveau passe à un autre état mental. Contrairement à ce qui se passe avec les bits informatiques, qui ne connaissent que les états on et off (1 et 0), le niveau d’activation d’un neurone est une variable continue, ce qui permet des variations et des nuances incroyablement subtiles des états mentaux (graphique 1).
Si les états mentaux sont produits par des structures d’activité neurale, alors la « connaissance », définie comme ce qui entraîne le flux cognitif d’un état mental à un autre, doit être encodée dans les connexions neurales. Cela signifie que l’apprentissage est le fait du développement de nouvelles synapses ou du renforcement ou de l’affaiblissement de synapses existantes. En fait, on a de bonnes raisons de penser que les deux mécanismes coexistent, le premier étant prédominant dans les cerveaux les plus jeunes et le second dans les cerveaux les plus mûrs. Il importe aussi de remarquer que, de ces deux faits, l’acquisition de nouvelles connaissances sur le long terme implique pour le cerveau une modification de son anatomie.
4.1.2. Organisation fonctionnelle - En matière de traitement de l’information, différentes parties du cerveau accomplissent différentes tâches. Ce principe de localisation fonctionnelle se vérifie à presque tous les niveaux de l’organisation cérébrale. Le cerveau est un ensemble de structures situé au sommet de la moelle épinière. Les structures inférieures sont affectées à la coordination de fonctions corporelles basiques (la respiration, la digestion, les mouvements volontaires, etc.), à l’expression des pulsions basiques (la faim, l’excitation sexuelle, etc.) et au traitement des émotions primaires (la peur, etc.). Les structures supérieures, qui ont évolué plus tard et par-dessus les structures inférieures, sont plus développées chez l’être humain que chez tout autre animal. La plus récente d’entre elles en termes d’évolution, le néocortex, est une mince couche de neurones recouvrant la surface des circonvolutions cérébrales. C’est le siège de la pensée, et c’est là que se trouvent les trois quarts des neurones du cerveau humain. Le néocortex se divise en deux hémisphères, le gauche et le droit. Entre les deux, un ruban de fibres neurales baptisé « corps calleux » sert de passerelle, permettant l’échange d’information entre les deux hémisphères. Chacun de ceux-ci est divisé en lobes, lesquels sont spécialisés et accomplissent des tâches différentes. Le lobe frontal (situé devant) se charge de l’action et de la planification. Le lobe temporal (sur le côté) se charge de l’audition, de la mémoire et de la reconnaissance des objets. Le lobe pariétal (en haut du crâne) se charge des sensations et du traitement de l’espace. Le lobe occipital (à l’arrière) se charge de la vision. Cette description est bien entendu fort grossière, chaque lobe étant subdivisé en réseaux de neurones imbriqués les uns dans les autres et affectés au traitement d’informations précises. Toute compétence complexe, comme l’addition ou la reconnaissance des mots, dépend de l’action coordonnée de plusieurs réseaux neuraux spécialisés localisés dans différentes parties du cerveau. Tout dégât infligé à l’un de ces réseaux ou aux connexions entre eux sera préjudiciable à la compétence qu’ils déterminent, et à chaque anomalie possible correspond un déficit bien précis (graphique 2).
Finalement, il convient de remarquer que deux cerveaux ne sont jamais parfaitement identiques. On rencontre des différences individuelles significatives en ce qui concerne la taille globale, mais aussi, ce qui est bien plus important, en ce qui concerne le nombre de neurones affectés à l’exécution de fonctions particulières, et même pour ce qui est de l’organisation et la localisation de modules fonctionnels. Comme la plupart des neurones sont interchangeables sur le plan fonctionnel, un même neurone peut être affecté à une tâche donnée, puis par la suite à une autre, ce qui signifie que la nature, la culture et l’apprentissage font inévitablement de chaque cerveau un cerveau unique, un chantier qui se prolonge durant toute la vie.
4.2. Outils de recherche, méthodologies et implications éducatives : l’impact de l’imagerie cérébrale - Les techniques de la recherche neuroscientifique sont variées et peuvent englober des processus dits invasifs (comme la neurochirurgie par exemple). Cependant, les outils les plus connus et les plus utilisés aujourd’hui relèvent de la technologie non invasive de l’imagerie cérébrale. Ces outils peuvent être séparés en deux catégories : ceux qui fournissent, sur l’activité cérébrale, une information spatiale de haute résolution et ceux qui fournissent une information temporelle de haute résolution. Parmi les outils fournissant une information spatiale de haute résolution, les plus connus sont la tomographie par émission de positons (TEP) et l’imagerie par résonance magnétique fonctionnelle (IRMf). Les techniques TEP détectent l’activité cérébrale au moyen de radio-isotopes en relevant les modifications dans la consommation d’oxygène et de glucose, et les altérations du flux sanguin cérébral. L’IRMf, par l’utilisation de fréquences radio et d’aimants, identifie les changements dans la concentration d’hémoglobine désoxygénée. Ces deux techniques demandent que le sujet conserve une immobilité parfaite pour que l’on parvienne à une imagerie exacte. La TEP et l’IRMf fournissant une résolution spatiale au millimètre près mais une résolution temporelle d’une précision de plusieurs secondes seulement, ces techniques sont utiles à la mesure des changements de l’activité cérébrale durant des phases d’activité cognitive relativement prolongées. Une autre technique, la stimulation magnétique transcrânienne (SMT), est utilisée pour créer une disruption temporaire (quelques secondes) des fonctions cérébrales afin d’aider à localiser l’activité cérébrale dans une région circonscrite du cerveau. Néanmoins, des processus tels que celui du calcul mathématique ou de la lecture impliquent plusieurs autres processus se produisant en l’espace de quelques centaines de millisecondes. Pour cette raison, la TEP et l’IRMf sont capables de localiser des régions du cerveau impliquées dans la lecture ou l’activité mathématique, mais ne peuvent mettre en lumière les interactions dynamiques entre processus mentaux durant ces activités. Un autre ensemble d’outils fournit une résolution temporelle à l’échelle de la milliseconde, mais la résolution spatiale est plus grossière, se limitant à quelques centimètres. Ces techniques mesurent les champs électrique ou magnétique à la surface du cuir chevelu durant l’activité mentale. Parmi elles figurent l’électroencéphalographie (EEG), les potentiels évoqués (ERP pour Event-Related Potentials) et la magnéto-encéphalographie (MEG). L’EEG et les ERP utilisent des électrodes placées en des endroits bien précis du crâne. Vu leur facilité d’utilisation et leur relative souplesse, ces techniques sont souvent utilisées avec succès chez les enfants. La MEG utilise des appareils fonctionnant à la température de l’hélium liquide, les SQUID (pour Super-Conducting Quantum Interference Devices). Grâce à ces outils, on peut effectuer des mesures exactes à l’échelle de quelques millisecondes dans les changements de l’activité cérébrale durant la réalisation de tâches cognitives. Parmi les nouvelles méthodes d’imagerie non invasive des fonctions cérébrales figure la topographie optique (OT pour Optical Topography), développée à partir de la spectroscopie en proche infrarouge (NIRS pour Near-Infrared Spectroscopy). Contrairement aux méthodologies conventionnelles, elle peut être utilisée pour des études de comportement, les fibres optiques flexibles permettant au sujet de conserver sa liberté de mouvement, de sorte qu’on peut construire un système aussi léger que compact. Cette méthode peut être appliquée à l’enfant comme à l’adulte. L’observation du développement lors du premier âge sur une durée d’un mois fournira des informations sur l’architecture du système des processus neuraux dans le cerveau. La topographie optique est susceptible d’avoir des répercussions très importantes sur l’éducation et l’apprentissage1. Pour procéder à des recherches efficaces dans le domaine de la neuroscience cognitive, il est nécessaire de combiner ces techniques afin de fournir des informations sur la localisation spatiale et les changements temporels de l’activité cérébrale associée à l’apprentissage. En opérant la liaison avec les processus de l’apprentissage, il est important pour le neuroscientifique de disposer d’opérations et d’analyses cognitives fines afin de tirer au maximum parti des outils d’imagerie cérébrale. Parmi les disciplines associées à l’apprentissage, celles qui fournissent le plus d’analyses fines du type recherché sont les études en science cognitive et en psychologie cognitive et, à ce jour, les études sur les processus visuels, la mémoire, le langage, la lecture, les mathématiques, et la résolution de problèmes. Parmi les autres options de recherche offertes aux neuroscientifiques, on trouve l’examen du cerveau lors d’une autopsie (pour mesurer la densité synaptique, par exemple) et, dans quelques rares cas, le travail auprès de certaines populations médicales, tels que les épileptiques par exemple (pour identifier les processus cérébraux auprès de personnes victimes de lésions ou de dommages cérébraux dus à une maladie ou à un traumatisme2). Certains neuroscientifiques étudient les enfants souffrant du syndrome d’alcoolisme foetal ou du syndrome du chromosome X fragile, d’autres la dégénérescence cognitive caractéristique du déclenchement de la maladie d’Alzheimer ou de la dépression sénile. D’autres encore étudient le cerveau des primates ou d’autres animaux, tels que les rats et les souris, afin de mieux comprendre le fonctionnement du cerveau humain. Par le passé, avant l’avènement des techniques d’imagerie cérébrale, il était difficile de collecter des informations d’essence neuroscientifique au sein de la partie saine de la population. Une autre limitation tient au fait qu’il n’existe pas un seul ensemble bien compris de tâches d’apprentissage ayant jamais été appliqué à des populations humaines normales sur toute la durée d’une vie. Un travail considérable a été accompli en ce qui concerne l’apprentissage lors de la petite enfance, beaucoup moins pour ce qui est de l’apprentissage pendant l’adolescence et encore moins à l’âge adulte. Sans schéma de référence du développement cognitif normal, il est difficile de comprendre une éventuelle pathologie de l’apprentissage. Nous devons comprendre à la fois le pouvoir et les limites des technologies d’imagerie cérébrale et la nécessité de protocoles cognitifs rigoureux si nous voulons commencer à comprendre comment la neuroscience cognitive peut guider l’éducation dans la formation de programmes d’études fondés sur les mécanismes cérébraux. De récentes découvertes commencent à montrer que l’éducation finira par se situer au carrefour de la neuroscience cognitive et de la psychologie cognitive tout en intégrant une analyse pédagogique sophistiquée et bien définie. A l’avenir, l’éducation sera transdisciplinaire, à la croisée de plusieurs domaines différents qui se fondront pour produire une nouvelle génération de chercheurs et de spécialistes de l’éducation aptes à poser des questions pertinentes et signifiantes au regard de l’éducation. Les méthodes de recherche actuelles en matière de neuroscience cognitive limitent nécessairement les types de problèmes étudiés. Par exemple, des questions comme : « Comment les individus apprennent-ils à reconnaître les mots écrits ? » sont plus ouvertes au traitement que « Comment les individus reconnaissent-ils les thèmes dans un texte ? », parce que l’objet de la première question mène à des études où les stimuli et les réponses sont plus faciles à contrôler et à contraster avec une autre tâche. En conséquence, le processus devient compréhensible en référence à des modèles cognitifs connus. L’objet de la seconde question implique trop de facteurs impossibles à séparer avec succès durant la phase expérimentale. Pour cette raison, les tâches éducatives valorisées par la société resteront toujours plus complexes que celles qui conviendraient sans doute à la neuroscience cognitive3. Les chercheurs soulignent aussi la nécessité méthodologique de tests d’apprentissage non seulement aussitôt après une intervention éducative (ce qui est typique des habitudes actuelles), mais aussi après un certain laps de temps, en particulier dans le cas d’une comparaison relative à l’âge4. Dans le cadre de telles études diachroniques, les projets de recherche quittent l’enceinte du laboratoire pour s’intéresser au vivant en situation réelle, ce qui induit une incertitude quant aux délais de disponibilité des résultats pour une interprétation dans un but éducatif.
4.3.3. Compétences mathématiques - La pensée mathématique, activité englobant la manipulation des nombres, est presque toujours difficile pour les enfants qui arrivent à l’école. Cependant, selon Stanislas Dehaene, les très jeunes enfants ont un sens inné des nombres, constituant une théorie élémentaire des nombres. La partie du cerveau responsable de cette capacité, le sillon intrapariétal, se spécialise dans la représentation de nombres en tant que quantités et permet aux très jeunes enfants de comprendre la différence entre « beaucoup » et « un peu ». Apprendre les mathématiques à l’école encourage les enfants à dépasser leurs talents innés pour l’approximation, à faire la distinction entre des nombres différents et à effectuer des manipulations et des opérations arithmétiques. De récentes recherches neuroscientifiques en matière d’apprentissage des mathématiques ont montré que le cerveau mettait en oeuvre différentes régions pour accomplir des tâches mathématiques différentes12. Le modèle du Triple Code13 suppose que pour trois manipulations arithmétiques de base, trois zones différentes du cerveau sont mises en oeuvre. Lorsque le sujet voit un nombre, par exemple « 3 », c’est le gyrus fusiforme qui est activé. Lorsqu’il entend ou lit le mot signifiant ce nombre, « trois », c’est la zone périsylvienne qui est active, et lorsqu’il comprend un nombre en tant que quantité, par exemple : « 3 est plus grand que 1 », ce sont les lobes interpariétaux qui interviennent. Grâce à ces recherches, scientifiques et éducateurs ont pu constater que les hémisphères du cerveau travaillaient ensemble plutôt que séparément14. Cependant, une lésion cérébrale, ou tout traumatisme entraînant une désorganisation des réseaux cérébraux, peut produire un désordre connu sous le nom d’acalculie ou dyscalculie (l’incapacité de calculer), les zones du cerveau citées cidessus n’étant pas activées normalement. Plus précisément, les enfants et les adultes souffrant de ce trouble sont incapables de comprendre la quantité signifiée par un nombre. Par exemple, ils ne parviendront pas à effectuer des opérations aussi simples que « 3 moins 1 », ni à déterminer quel est le nombre compris entre 2 et 4. En d’autres termes, ils auront perdu le concept spatial de quantité. Outre les lésions cérébrales ou les désordres neurologiques, les chercheurs supposent l’existence de deux autres causes différentes aux difficultés mathématiques. Primo, un réseau tel que celui qui est associé à la quantité peut être déficient ou désorganisé, de sorte que le sujet a des difficultés à accéder aux informations sur l’inclusion des nombres. Autre cause possible, sans doute plus courante : l’enfant n’a pas encore appris à connecter la représentation d’une quantité avec des symboles verbaux et visuels. Cette tâche peut lui être difficile, car la pensée ou les transformations symboliques s’acquièrent avec l’expérience, tant éducative que culturelle. Comme dans le cas de la dyslexie, précédemment mentionné, le modèle neuroscientifique de Stanislas Dehaene fournit pour les compétences mathématiques une décomposition en tâches qui peut être utilisée pour concevoir ou valider des approches pédagogiques. Entre autres, la dissociation entre représentation de la quantité et système verbal va dans le sens de l’hypothèse d’une pensée sans langage, ce qui signifie que le matériel pédagogique employant une métaphore spatiale ou concrète de l’ensemble des nombres (comme la droite des nombres ou le boulier chinois), est sans doute particulièrement adapté à l’enseignement du sens des nombres. Illustration de l’efficacité de l’enseignement des mathématiques par l’accès au système de représentation de la quantité, le programme Right Start15 enseigne des compétences arithmétiques basiques telles que le comptage, les correspondances entre les nombres et les quantités, et le concept de la droite des nombres. Ce programme fait découvrir aux enfants un analogue spatial de l’ensemble des nombres en utilisant des objets concrets tels que le jeu de l’oie16. Ce type de formation connaît une telle réussite pour ce qui est de la remédiation qu’après 40 séances de 20 minutes chacune, certains enfants à l’origine en difficulté atteignent un niveau supérieur à celui des élèves du même âge connaissant un développement normal en mathématiques.
NOTES - 1. Koizumi, H. et al. (1999), « Higher-order brain function analysis by trans-cranial dynamic near-infrared spectroscopy imaging », Journal Biomed. Opt., vol. 4, couv. et pp. 403-413.
2. Luis Fuentes a évoqué durant le Forum de Grenade (voir Rapport de Grenade, site web de l’OCDE, op. cit.) le problème de la corrélation entre les théories neurales de l’esprit et les fonctions cognitives du cerveau, ainsi qu’une approche de l’étude de l’apprentissage insistant sur la décomposition des tâches et encourageant l’étude de tâches cognitives toutes simples dont on pense qu’elles impliquent l’orchestration d’opérations élémentaires bien localisées dans le cerveau. Durant les 40 dernières années, on a utilisé ces méthodes pour montrer comment les gens lisent, écrivent, visualisent, reconnaissent les objets, etc. L’étude de patients souffrant de lésions cérébrales tend à confirmer l’idée selon laquelle différentes parties du cerveau effectuent différentes opérations. Par exemple, les patients atteints d’agnosie visuelle ont des difficultés à reconnaître les visages non altérés alors que leurs capacités visuelles sont par ailleurs intactes. Certains patients reconnaissent les exemples d’une catégorie sémantique bien précise sans en reconnaître d’autres. Luis Fuentes est d’avis que cette accumulation de preuves exige que les systèmes cognitifs soient découplés en opérations élémentaires. « Les études effectuées sur les primates, puis sur les patients affectés par des lésions du cortex pariétal, démontrent que la conscience dépend de l’orchestration de trois opérations différentes engagées dans l’altération de l’attention : le désengagement, le mouvement et l’engagement de l’attention, ces trois opérations étant effectuées respectivement par le lobe pariétal postérieur, le colliculus supérieur et le noyau du pulvinar du thalamus. Lorsqu’un patient présente une lésion dans l’une de ces parties du cerveau, il néglige les stimuli apparaissant du côté opposé à celui de la lésion. En d’autres termes, il perd conscience des informations présentées à cette partie de l’espace visuel en dépit [du fait] qu’il n’a aucun autre problème visuel. »
12. Comme l’a rapporté Diego Alonso durant le Forum de Grenade, les études du comportement comme celles de l’imagerie du cerveau suggèrent que le traitement de l’arithmétique sollicite le lobe frontal gauche (une région en général active durant les tâches mémorielles verbales), et que d’un autre côté, les estimations arithmétiques impliquent les lobes pariétaux inférieurs droit et gauche (des zones associées à des tâches visuelles et spatiales). Le cortex préfrontal et le cortex cingulaire antérieur jouent un rôle important lors des calculs complexes en contrôlant les stratégies non automatisées. Il faut cependant noter que, lors d’un traitement mathématique, d’autres zones du cerveau sont impliquées, en plus de celles mentionnées ci-dessus. Sur un plan plus spéculatif, Diego Alonso a signalé les travaux de George Lakoff et Rafael Nuñez, qui suggèrent des voies de recherche possibles pour la neuroscience cognitive : jusqu’à quel point les gens utilisent-ils des schémasimages (c’est-à-dire des concepts faisant appel aux relations spatiales telles que l’inclusion, le contact, l’opposition centre/périphérie, etc.) et des métaphores conceptuelles (recouvrement d’une intersection préservant des structures inférentes) pour créer et comprendre les concepts mathématiques ? (voir le rapport de Grenade, site web de l’OCDE, op. cit.).
13. Le modèle de Dehaene décrit un système de zones du cerveau actives lorsque l’enfant apprend ou effectue des opérations arithmétiques. Pour plus de détails, voir Dehaene, S., Spelke, E., Pinel, P., Stanescu, R., et Tsivlin, S. (1999), « Sources of mathematical thinking : Behavioural and brain imaging evidence », Science, vol. 284, no 5416, pp. 970-974.
14. Voir : « Spécialisation hémisphérique », 4.6.2 infra
15. « The Right Start Programme » – voir Dehaene, S. (1996), La bosse des maths, Éditions Odile Jacob.
16. En anglais, Snakes and Ladders (« Serpents et échelles »). Il s’agit à l’origine d’un jeu asiatique du nom de Parcheesi, un jeu de moralité (les échelles conduisant à des niveaux supérieurs du bien et les serpents barrant l’accès à ces niveaux). Ce jeu existe toujours, en Orient comme en Occident, mais le joueur utilise désormais ses compétences mathématiques pour gagner le plus de points possible. [OCDE 2000:52]
[1] «L'idée vague de continuité, que nous devions à l'intuition, s'est résolue en un système compliqué d'inégalités portant sur des nombres entiers. Par là, les difficultés provenant des passages à la limite, ou de la considération des infiniment petits, se sont trouvées définitivement éclaircies. Il ne reste plus aujourd'hui en Analyse que des nombres entiers ou des systèmes finis ou infinis de nombres entiers, reliés entre eux par un réseau de relations d'égalité ou d'inégalité. Les Mathématiques, comme on a dit, se sont arithmétisées. [...] Dans l'Analyse d'aujourd'hui, quand on veut se donner la peine d’être rigoureux, il n'y a plus que des syllogismes ou des appels à cette intuition du nombre pur, la seule qui ne puisse nous tromper. On peut dire qu'aujourd'hui la rigueur absolue est atteinte» [Poincaré 1905 : 32-33]